Question

Prove that 2x^2+x+8>0 for all real values of x.

Answer 1

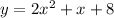
`y = 2x^2 + x + 8` is a polynomial of even degree, with a positive
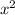
`x^2` coefficient, meaning that
- it will have exactly one turning point
- that turning point will be a minimum

So, if the y-coordinate of the turning point is positive, then this polynomial will be positive for all real values of x.

At a turning point, the gradient of y will be equal to 0. The gradient of y is given by

`\frac{\mathrm{d}y}{\mathrm{d}x} = 4x + 1`.

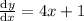
To find the turning point, set this equal to 0 and solve for x:

`4x + 1 = 0 \implies x = -(1)/(4)`.

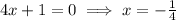
Substituting this value into the equation gives

`y = 2(-(1)/(4))^2 + (-(1)/(4)) + 8 = (1)/(4) - (1)/(4) + 8 = 8 \ \textgreater \ 0`.

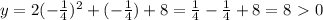
Since the minimum point of the equation is greater than 0, the equation will be greater than 0 for all real values of x.