Question

Use the method of completing the square to transform the quadratic equation into the equation form (x + p)^2 = q.

3 + x - 3x^2 = 9

Answer 1

We have that

`-3x^2 + x + 3 = 9`.

First we should transform it so that the left hand side is equal to 0, and the
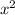
`x^2` coefficient (that is, the number of
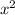
`x^2`s you have) is equal to 1.

So first we will subtract 9, giving

`-3x^2 + x -6 = 0`.

Now we will multiply by -1, giving

`3x^2 - x + 6 = 0`,

and finally we will divide by 3 to make the
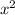
`x^2` coefficient equal to 1, giving

`x^2 - (1)/(3)x + 2 = 0`.

Now it is the form we need to complete the square. Notice that expanding
`(x+p)^2` gives

`x^2 + 2px + p^2.`

Now, we have
`(1)/(3) x` in our equation so we want

`2p = (1)/(3) \implies p = (1)/(6)`.

If
`p = (1)/(6)` then, from our expansion above, we have that

`(x+(1)/(6))^2 = x^2 + (1)/(3)x + (1)/(36)`,
which is almost our equation, but not quite. Instead of
`(1)/(36)`, we have 2. So we need to add
`(71)/(36)`, giving:


`(x+(1)/(6))^2 + (71)/(36) = x^2 + (1)/(3)x + 2 = 0`.


So, finally, subtracting the
`(71)/(36)`, we have


`(x+(1)/(6))^2 = -(71)/(36)`

which is in the required form.