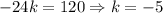It is known that x and y are roots of the equation 6x^2 +7x +k =0, where 2x +3y =-4. Find k

Question

It is known that x and y are roots of the equation


`6x^2 +7x +k =0`, where
`2x +3y =-4`.
Find k

Answer 1

Explanation:

We are going to express

y in terms of x.

=> 2x + 3y = -4, y = (-4 - 2x)/3.

By Vieta's Formula,

We have SOR = -b/a and POR = c/a.

=> x + y = -7/6, xy = k/6.

When x + y = -7/6,

x + (-4 - 2x)/3 = -7/6.

=> (x - 4)/3 = -7/6

=> (x - 4) = -7/2

=> x = 4 - 7/2

=> x = 0.5.

When xy = k/6,

x(-4 - 2x)/3 = k/6.

Hence k = 6[x(-4 - 2x)/3]

= 2x(-4 - 2x) = 2(0.5)(-4 - 2(0.5)) = -5.

The value of k is -5.

Answer 2

`k = -5`

Explanation:

We have the quadratic equation:

`6x^2+7x+k=0`

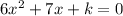
Where x and y are the roots of the equation and:

`2x+3y=-4`

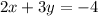
First, using the quadratic formula with a = 6, b = 7, and c = k, we can find the roots to be:

`\displaystyle x=(-(7)\pm√((7)^2-4(6)(k)))/(2(6))`

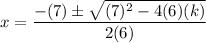
Simplify:

`\displaystyle x=(-7\pm√(49-24k))/(12)`

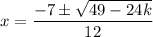
So, our two roots are:

`\displaystyle x=(-7+√(49-24k))/(12)\text{ and } y=(-7-√(49-24k))/(12)`

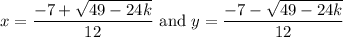
For our first root, we can multiply both sides by 2.

And for our second root, we can multiply both sides by 3.

So, this produces:

`\displaystyle 2x=(-7+√(49-24k))/(6)\text{ and } 3y=(-7-√(49-24k))/(4)`

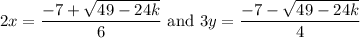
Since we are given that:

`2x+3y=-4`

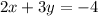
By substitution:

`\displaystyle \Big((-7+√(49-24k))/(6)\Big)+\Big((-7-√(49-24k))/(4)\Big)=-4`

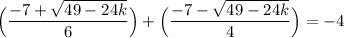
Remove the fractions by multiplying both sides by 12:

`\displaystyle (-14+2√(49-24k))+(-21-3√(49-24k))=-48`

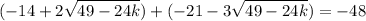
Combine like terms:

`-35-√(49-24k)=-48`

Adding 35 to both sides produces:

`-√(49-24k)=-13`

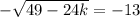
So:

`√(49-24k)=13`

Squaring produces:

`49-24k=169`

Therefore:

`-24k=120\Rightarrow k=-5`