First let's draw the triangle PQR:
In order to find the length of QR, we can use the sine relation of the angle P.
The sine relation is given by the length of the opposite side to the angle over the length of the hypotenuse.
So we have that:
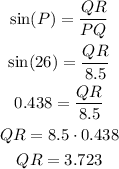
Rounding to the nearest tenth, the length of QR is 3.7 feet.