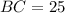Question

If the triangle shown, The angle CAB = 30° and AC =50m. What is the length of BC is?

Answer 1

GIVEN:

We are given a right angle as shown in the attached image. For triangle ABC, we have;

`\angle A=30\degree,\text{ }AC=50m`

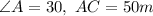
Required;

To find the length of side AC.

Step-by-step solution;

For a right angled triangle with respect to the reference angle, the sides are labeled as follows;

`\begin{gathered} Reference\text{ }angle=30\degree \\ \\ Opposite=BC \\ \\ Adjacent=AB \\ \\ Hypotenuse=AC \end{gathered}`

To find the length of BC (opposite), given the length of AC (hypotenuse), we shall use the ratio;

`sin\theta=(opposite)/(hypotenuse)`

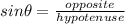
We now use the values provided and we have;

`sin30\degree=(BC)/(50)`

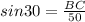
Now we cross multiply;

`\begin{gathered} 50* sin30=BC \\ \\ 50*0.5=BC \\ 25=BC \\ \end{gathered}`

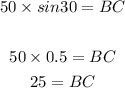
ANSWER:

`BC=25`