Question

Determine the equation of this degree 5 polynomial? Much appreciated

Answer 1

From the graph we can see

There are 3 exact zeroes

x = -4

x = -1

x = 1

Then there are 3 factors

(x + 4), (x + 1), (x - 1)

Then we will let the other 2 factors are (x - a) and (x - b)

Then we will use the exact vertices (2, 3) and (4, -3) to find a and b

`y=(x+4)(x+1)(x-1)(x-a)(x-b)`

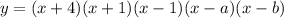
We will start by multiplying (x - 1) by (x + 1)

`(x-1)(x+1)=x^2-1`

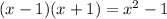
Now, multiply the answer by (x + 4)

`(x^2-1)(x+4)=x^3+4x^2-x-4`

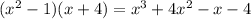
Multiply this answer by (x - a)

`\begin{gathered} (x-a)(x^3+4x^2-x-4)=x^4+4x^3-x^2-4x-ax^3-4ax^2+ax+4a= \\ x^4+(4-a)x^3-(1+4a)x^2+(a-4)x+4a \end{gathered}`

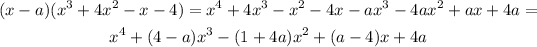
Then the polynomial is

`y=[x^4+(4-a)x^3-(1+4a)x^2+(a-4)x+4a](x-b)`

Substitute y by 3 and x by 2 (one of the vertex (2, 3))

`\begin{gathered} 3=[16+(4-a)8-(1+4a)4+(a-4)2+4a](2-b) \\ 3=[16+32-8a-4-16a+2a-8+4a](2-b) \\ 3=[36-18a][2-b] \end{gathered}`

Multiply the 2 brackets

`\begin{gathered} 3=72-36b-36a+18ab \\ 36a+36b-18ab=69\rightarrow Divide\text{ by 3} \\ 12a+12b-6ab=23\rightarrow(1) \end{gathered}`

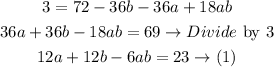
We will substitute y by -3 and x by 4 (the second vertex (4, -3)

`\begin{gathered} -3=[256+(4-a)64-(1+4a)16+(a-4)4+4a][4-b] \\ -3=[256+256-64a-16-64a+4a-16+4a][4-b] \\ -3=[480-120a][4-b] \end{gathered}`

Multiply the 2 brackets

`\begin{gathered} -3=1920-480b-480a+120ab \\ 480a+480b-120ab=1923 \\ 160a+160b-40ab=641\rightarrow(2) \end{gathered}`

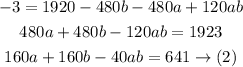
Now we need to solve equations (1) and (2) to find a and b

`\begin{gathered} -(40)/(3)(12a)-(40)/(3)(12b)-(40)/(3)(-6ab)=-(40)/(3)(23) \\ -160a-160b+80ab=-(920)/(3)\rightarrow(3) \\ Add(2),(3) \\ 40ab=(1003)/(3) \\ \\ ab=(1003)/(120) \end{gathered}`

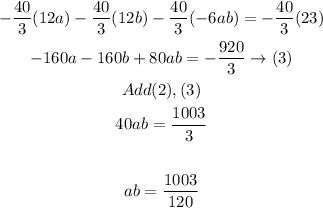
Then substitute the value of ab

`\begin{gathered} (x-a)(x-b)=x^2-bx-ax+ab \\ =(x^2-bx-ax+(1003)/(120)) \\ y=(x^3+4x^2-x-4)(x^2-ax-bx+(1003)/(120)) \end{gathered}`

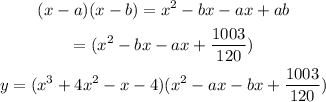
Substitute x by -2 and y by 0 (y-intercept)

`\begin{gathered} 0=(-8+16+2-4)(4+(a+b)2+(1003)/(120)) \\ 0=6(4+2(a+b)+(1003)/(120)) \\ 0=24+12(a+b)+(1003)/(20) \\ a+b=-(1483)/(240) \end{gathered}`
`y=(x^3+4x^2-x-4)(x^2+(1483)/(240)x+(1003)/(120))`

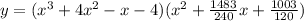
We can simplify it by multiplying the 2 brackets to get the final form of the equation

`y=x^5+(2443)/(240)x^4+(1283)/(40)x^3+(5581)/(240)x^2-(1323)/(40)x-(1003)/(30)`

This is the final answer of the polynomial of the 5th degree