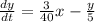Question

ank A contains 80 gallons of water in which 20 pounds of salt has been dissolved. Tank B contains30 gallons of water in which 5 pounds of salt has been dissolved. A brine mixture with a concentrationof 0.5 pounds of salt per gallon of water is pumped into tank A at the rate of 4 gallons per minute.The well-mixed solution is then pumped from tank A to tank B at the rate of 6 gallons per minute.The solution from tank B is also pumped through another pipe into tank A at the rate of 2 gallonsper minute, and the solution from tank B is also pumped out of the system at the rate of 4 gallons perminute. Find the differential equations with initial conditions for the amounts,x(t)andy(t), of saltin tanks A and B, respectively, at time t.

Answer 1

`(dx)/(dt)=2-(3)/(40)x+(y)/(15)`

`(dy)/(dt)=(3)/(40)x-(y)/(5)`

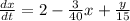
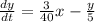
x(0)=20,y(0)=5

Explanation:

We are given that

Tank A contains water=80 gallons

x(0)=20,y(0)=5

Tank B contains water=30 gallons

Rate=4 gallon/min

Concentration of salt is pumped into tank=0.5 pound /gallon of water

Solution pumped from tank A to tank B at the rate=6 gallons/min

Solution pumped from tank B to tank A at the rate=2gallon/min

Solution from tank B is pumped out of the system at the rate=4 gallon/min

We have to find the DE at time t

For x

Rate in=
`0.5* 4+y(t)/30* 2`

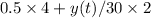
Rate in=
`2+y/15`

Rate out=
`x/80* 6`

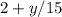
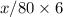
Rate out=3x/40[/tex]

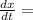`(dx)/(dt)=`Rate in-Rate out

`(dx)/(dt)=2+y/15-3x/40`

`(dx)/(dt)=2-(3)/(40)x+(y)/(15)`

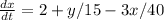
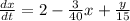
For y

Rate in=
`x/80* 6`

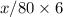
Rate in=3/40x

Rate out=
`y/30* (4+2)`

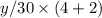
Rate out=y/5

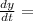`(dy)/(dt)=`Rate in-Rate out

`(dy)/(dt)=(3)/(40)x-(y)/(5)`