Answer:
5x - 3y = 30
Step-by-step explanation:
In the question we were told that the line CD passes through the points C (3,-5) and D(6,0) that is (
 ,
,
 ) and (
) and (
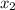 ,
,
 ) , From the options given we can tell that the equation is the equation of a straight line.
) , From the options given we can tell that the equation is the equation of a straight line.
The general equation of a straight line is y = mx + c, where m is the gradient, and y = c is the value where the line cuts the y-axis. This number c is called the intercept on the y-axis. The equation of a straight line with gradient m and intercept c on the y-axis is y = mx + c.
But in our explanation we will replace C in the general equation with D to avoid confusion as the question already has C and D as coordinates.
The general equation for a straight line is of the form y = mx + E. We will first find the value of m, substitute it into the general equation to get the value of D. From resulting equation gotten from substituting the value of D, we can then obtain the desired equation.
Finding the slope m of the line y =mx + E
substituting values of the points C (3,-5) and D(6,0) into (
 ,
,
 ) and (
) and (
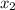 ,
,
 ) in the equation below.
) in the equation below.
m =

m =
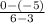
m =
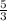
Finding the intercept E of the line y =mx + E
Now substitute the value of the slope m and the first coordinates C(3, -5) into the straight line equation y= mx + E
-5 =
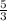 *3 + E
*3 + E
We have E = -10
Finding the equation
Substitute the value of E= -10 and m = 5/3 into the straight line equation y =mx + E
We have y =
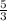 *x -10
*x -10
Multiply both sides of the equation by 3
3y = 5x -30
rearranging the equation in the Ax + Bx + C = 0
we have
5x – 3y =30 as the correct answer.