Question

A device for acclimating military pilots to the high accelerations they must experience consists of a horizontal beam that rotates horizontally about one end while the pilot is seated at the other end. In order to achieve a radial acceleration of 32.7 m/s2 with a beam of length 5.29 m , what rotation frequency is required

Answer 1

The rotation frequency required is 23.78 RPM

Step-by-step explanation:

Given;

radial acceleration, a = 32.7 m/s²

length of the beam, r = 5.29 m

The linear velocity is calculated as;

`a = (v^2)/(r) \\\\v^2 = ar\\\\v = √(ar)`

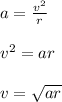
where;

v is linear velocity

The angular velocity is calculated as;

`\omega = (v)/(r) \\\\Recall, v = √(ar) \\\\Then, \omega = (√(ar))/(r)} \\\\ \omega = (√(32.7 *5.29))/(5.29)\\\\\omega = 2.49 \ rad/s\\\\Angular \ frequency \ is \ calculated \ as;\\\\\omega = 2\pi f\\\\f = (\omega)/(2\pi) \\\\f = (2.49)/(2\pi) \\\\f = 0.396 \ rev/s\\\\f = 23.78 \ rev/min`

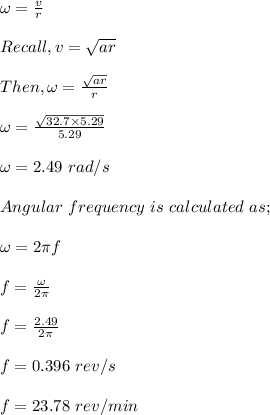
Therefore, the rotation frequency required is 23.78 RPM