Given:
Expect to receive = $10000
Rate = 8%
Final amount = $95000
Find-:
How long will you wait
Explanation-:
Value after some time is:
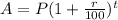
Where,

So, the value is:
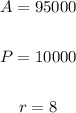
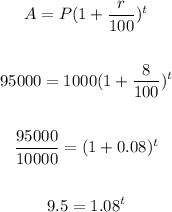
For time taking log both sides.
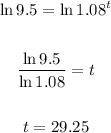
Hence time wait from now:
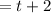
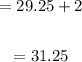
So the total time is 31.25 years.