Given the following equation,
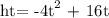
Where,
h(t) = the height of the ball at the given time
t = time
Since we are asked to look for the time when the ball is higher than 12 feet off the ground, it should also mean that we are going to find t at h(t) = 12.
We get,
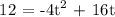
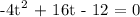
a = -4
b = 16
c = -12
Let's apply the Quadratic Formula:
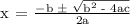
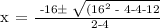
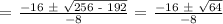
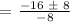
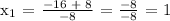
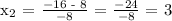
Therefore, the time when the ball is higher than 12 feet off the ground is between t = 1 and t = 3.
Putting that into an inequality will be: 1 < t < 3
The answer is CHOICE C : 1 < t < 3