Question

The probability that a comic book reader in a particular city prefers comics published by Company A is 25%. The probability that a comic book reader in the city is male is 70%. If the probability of a comic book reader in the city being a male, given that the reader prefers Company A's comics, is 40%, what is the probability of the reader preferring Company A's comics, given that the reader is a male?

Answer 1

Probability of the reader preferring Company A's comics, given that the reader is a male -0.14

Explanation:

Given : Comic published by Company A =25% ⇒
`P(A)=(25)/(100)=0.25`

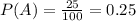
Probability that a comic book reader is male=70% ⇒
`P(M)=(70)/(100)=0.7`

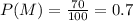
Probability of a comic book reader in the city being a male, given that the reader prefers Company A's comics= 40% ⇒
`P(A/M)=(40)/(100)=0.4`

To find : Probability of the reader preferring Company A's comics, given that the reader is a male =
`P(M/A)`

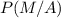
Solution : Using Bayes' theorem, which state that

`P(A/B)=(P(B/A)P(A))/(P(B))`

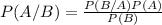
where, P(A) and P(B) are probabilities of observing A and B.

P(B/A)= is a conditional probability where event B occur and A is true

P(A/B)= also a conditional probability where event A occur and B is true.

Now, applying Bayes' theorem,

`P(M/A)=(P(A/M)P(A))/(P(M))`

`P(M/A)=((0.4)(0.25))/(0.7)`

`P(M/A)=(0.1)/(0.7)`

`P(M/A)=0.14`

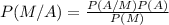
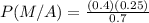
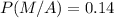
Therefore, Probability of the reader preferring Company A's comics, given that the reader is a male -0.14