Step 1
State the formula for the volume of a cone.

Where;
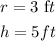
Step 2
Find the volume of the cone in the figure.
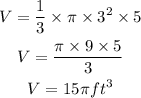
Step 3
State the formula for the volume of a cylinder
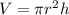
where;
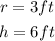
Step 4
Find the volume of the cylinder.

The total volume of the figure is, therefore;

The total volume of the figure in terms of π=69π cubic feet
Answer;69π cubic feet