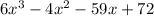Question

multiply the following polynomials and write the resulting polynomial in descending order. (3x-8)(2x^2+4x-9)

Answer 1

Given the polynomial:
`(3x-8)(2x^2+4x-9)`

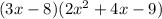
Since, arranging of polynomial can be made by forming the given polynomial into the general form.

Multiply the following polynomials are;

`(3x)(2x^2+4x-9)-8(2x^2+4x-9))`

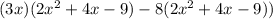
Using distributive property:
`a\cdot(b+c) = a\cdot b+a\cdot c`

`(6x^3+12x^2-27x)- (16x^2+32x -72)`

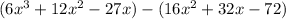
Remove the parenthesis; we get;

`6x^3+12x^2-27x- 16x^2 -32x +72`

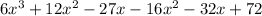
Combine like terms;

`6x^3-4x^2-59x+72`

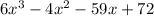
⇒This is the general form of the polynomial equation.

Since, the given polynomials can be written from the order of powers i.e,

`6x^3-4x^2-59x+72`

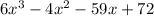
To arrange this polynomial in descending order means to arrange the powers of variables in each term in descending order.

Therefore, the resulting polynomial in descending orders is,
`6x^3-4x^2-59x+72`