Question

Find the distance between the complex numbers in the complex plane.7i, 4 − 3i

Answer 1

Given:

There are given two complex number is:

`7i,4-3i`

Step-by-step explanation:

According to the question:

We need to find the value of the distance between two complex numbers.

Then,

From the given complex number:

`7\imaginaryI,4-3\imaginaryI`

That means, the point is:

`(0,7),and,(4,-3)`

Now,

From the distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

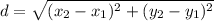
Where,

`x_1=0,y_1=7,x_2=4,y_2=-3`

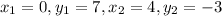
Then,

`\begin{gathered} d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ d=√((4-0)^2+(-3-7)^2) \\ d=√((4)^2+(-10)^2) \end{gathered}`

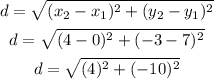
Then,

`\begin{gathered} d=√((4)^2+(-10)^2) \\ d=√(16+100) \\ d=√(116) \end{gathered}`

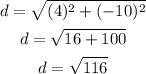
Final answer:

Hence, the value of the distance is shown below:

`d=√(116)`