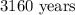Question

Radiocarbon dating of a sample of wood from the tomb of an Egyptian pharaoh found that in 1 of the sample there were 9.843 × 10−15 of C-14 and 1.202 × 10−2 of C-12. The C-14 isotope is radioactive and undergoes − decay with a half-life of 5,730 years; the C-12 isotope is stable (does not decay). If the initial ratio of these isotopes is known to be −14 = 1.20 × 10−12, how old is the sample of wood in the tomb?

Answer 1

Let C be the total amount of C-14, after a time t from the origin of the piece of wood. If the initial amount of C-14 is C_0, and the half-life of C-14is τ, then, the formula that relates these variables, is:

`C=C_0*2^(-t/\tau)`

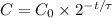
Isolate t from the equation:

`\begin{gathered} \Rightarrow(C)/(C_0)=2^(-t/\tau) \\ \Rightarrow\log _2((C)/(C_0))=-(t)/(\tau) \\ \Rightarrow-\tau\cdot\log _2((C)/(C_0))=t \end{gathered}`

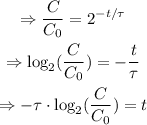
Therefore:

`t=-\tau\cdot\log _2((C)/(C_0))`

Since the ratio r between the initial amount of C-14 and C-12 is given, we can find the initial amount of C-14:

`\begin{gathered} (C_0)/(C_(12))=r \\ \Rightarrow C_0=r* C_(12) \end{gathered}`

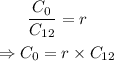
Substitute r=1.20*10^-12 and C_12=1.202*10^-2 mol to find the initial amount of C-14:

`\begin{gathered} C_0=1.2*10^(-12)*1.202*10^(-2)\text{mol} \\ =1.4424*10^(-14)\text{mol} \end{gathered}`

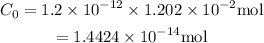
Substitute τ=5730y, C_0=1.4414*10^-14 mol, and C=9.843*10^-15 mol into the formula to find t, which is the age of the wood from the sample:

`\begin{gathered} t=-\tau\cdot\log _2((C)/(C_0)) \\ =-5730y*\log _2(\frac{9.843*10^(-15)\text{mol}}{1.4424*10^(-14)\text{mol}}) \\ =3158.956\ldots y \end{gathered}`

Therefore, to the nearest ten, the age of the sample of wood in the tomb, is:

`3160\text{ years}`