Question

Not really how to do this, but I need some help

Answer 1

Given a polynomial of the form:

`x^2+bx+c`

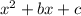
The method of completing the square give us another expression for that polynomial:

Where k is given by:

`k=c-(b^2)/(4)`

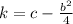
So first we have to identify b and c:

`\begin{gathered} x^2+14x=-69 \\ x^2+14x+69=0 \\ x^2+14x+69=x^2+bx+c \end{gathered}`

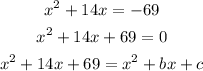
Then b=14 and c=69. This means that by completing the square we get:

`\begin{gathered} x^2+14x+69=(x+(b)/(2))^2+c-(b^2)/(4) \\ x^2+14x+69=(x+(14)/(2))^2+69-(14^2)/(4) \\ (x+(14)/(2))^2+69-(14^2)/(4)=(x+7)^2+69-49 \\ (x+7)^2+69-49=(x+7)^2+20 \end{gathered}`

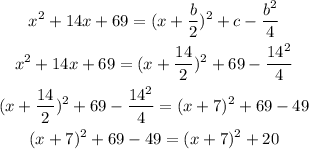
So we have:

`\begin{gathered} x^2+14x+69=(x+7)^2+20 \\ \text{And} \\ x^2+14x+69=0 \end{gathered}`

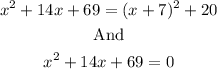
Which means that:

`\begin{gathered} (x+7)^2+20=0 \\ (x+7)^2=-20 \\ x+7=\pm\sqrt[]{-20}=\pm i\sqrt[]{20}=\pm2i\sqrt[]{5} \\ x=-7\pm2i\sqrt[]{5} \end{gathered}`

Which means that the answer is the second option.