Answer:
Approximately
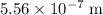 in this glass.
in this glass.
Step-by-step explanation:
The frequency of a wave is the number of periods that this wave completes per unit time.
The speed of a wave is the distance that this wave travels in unit time.
Thus, dividing the speed
 of the wave by the frequency
of the wave by the frequency
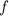 of this wave would give the distance that this wave covers in each period (cycle) of this wave. By definition, the distance that a wave covers in each period is precisely the wavelength of this wave. Therefore, an equation for the wavelength
of this wave would give the distance that this wave covers in each period (cycle) of this wave. By definition, the distance that a wave covers in each period is precisely the wavelength of this wave. Therefore, an equation for the wavelength
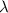 of a wave would be:
of a wave would be:
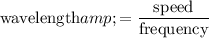 .
.
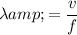 .
.
Note that
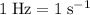 .
.
The wavelength of this light in this glass would be:
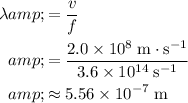 .
.