Question

May you solve for part a and part b please

Answer 1

`\begin{gathered} \sin 2\theta=-\frac{5\text{ }\sqrt[]{119}}{72} \\ \\ \cos (\theta)/(2)=\frac{\sqrt[]{102}}{12} \end{gathered}`

θ/2 lies in the first quadrant.

STEP - BY - STEP EXPLANATION

What to find?

• sin2θ

,

• cos θ/2

,

• The quadrant in which angle θ/2 is located.

Given:

cosθ =5/12

3π/2 <θ < 2π

Part A : Finding the value of sin2θ

To find the value of sin2θ, we will need to first recall the formula for double angles.

This is given below:

sin2θ = 2sinθcosθ.

Proceed to find the value of sinθ using the formula the trigonometric identity given below:

sin²θ + cos²θ = 1

Substitute cosθ= 5/12 into the above and solve for sinθ.

`\begin{gathered} \sin ^2\theta+((5)/(12))^2=1 \\ \\ \sin ^2\theta+(25)/(144)=1 \\ \\ \sin ^2\theta=1-(25)/(144) \\ \\ \sin ^2\theta=(144-25)/(144)=(119)/(144) \\ \\ \sin \theta=\pm\sqrt[]{(119)/(144)}=\frac{\pm\sqrt[]{119}}{12} \end{gathered}`

Since θ is between 3π/2 and 2π ( that is between 270 and 360)

This implies θ is in the 4th quadrants.

Observe that only cosθ is positive in the fourth quadrant. This implies sinθ is negative in quadrant IV, Hence we take only the negative value of sinθ.

sinθ = -√119 / 12

We can now go ahead and solve for sin2θ using our formula.

sin2θ = 2sinθcosθ.

Substitute the values and simplify.

`\sin 2\theta=2((5)/(12))(-\frac{\sqrt[]{119}}{12})`
`=(5)/(6)*-\frac{\sqrt[]{119}}{12}`
`=-\frac{5\text{ }\sqrt[]{119}}{72}`

Therefore sin2θ = -5√119 / 72

Part B : Finding the value of cos θ/2

We can determine cos θ/2 using the half angle formula given below:

cosθ = 2cos²θ / 2 - 1

Make cosθ/2 subject of formula.

Add 1 to both-side of the equation.

`2\cos ^2(\theta)/(2)=\cos \theta+1`

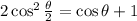
Divide both-side of the equation by 2.

`\cos ^2(\theta)/(2)=(\cos \theta+1)/(2)`

Take square root of both-side.

`\cos (\theta)/(2)=\sqrt[]{(\cos\theta+1)/(2)}`

Now substitute the value of cosθ and simplify.

`\begin{gathered} \cos (\theta)/(2)=\sqrt[]{((5)/(12)+1)/(2)} \\ \\ =\sqrt[]{((5+12)/(12))/(2)} \\ \\ =\sqrt[]{((17)/(12))/(2)} \\ \\ =\sqrt[]{(17)/(12)*(1)/(2)} \\ \\ =\sqrt[]{(17)/(24)} \end{gathered}`

Rationalize.

`=\frac{\sqrt[]{17}}{\sqrt[]{24}}*\frac{\sqrt[]{24}}{\sqrt[]{24}}`
`=\frac{\sqrt[]{408}}{24}=\frac{2\sqrt[]{102}}{24}=\frac{\sqrt[]{102}}{12}`

Therefore, cos θ/2 = √102 / 12

Determine the quadrant of θ/2

Take the arccos of both-side.

`(\theta)/(2)=\cos ^(-1)(\frac{\sqrt[]{102}}{12})`

`(\theta)/(2)\approx32.7\degree`

Hence, θ/2 lies in the first quadrant.