For two lines to be parallel,
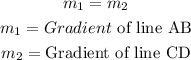
For two lines to be perpendicular,
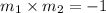
The formula for the gradient of a line passing through points (x1,y1) and (x2,y2) is given as

For line AB, the point given is
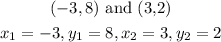
By substituting in the formula, we will have
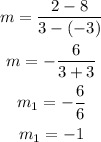
For line CD, the point given is

By substituting the values in the formula, we will have
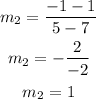
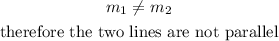

Therefore,
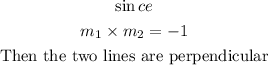
Hence,
Line AB and line CD are perpendicular