Question

Use the difference of two squares theorem to find the solution to each equation

Answer 1

We will investigate how to use the difference of two squares theorem to determine a solution to the equation.

The equation at hand is as follows:

`(\text{ x + }(1)/(7))^2\text{ = 8}`

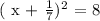
We will move all the terms on the left hand side of the " = " sign as follows:

`(\text{ x + }(1)/(7))^2\text{ - 8 = 0}`

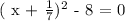
The difference of two squares theorem states that:

`a^2-b^2\text{ = ( a + b ) }\cdot\text{ ( a - b )}`

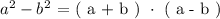
We see from the above form that we have the following:

`\begin{gathered} a\text{ = x + }(1)/(7) \\ \\ b\text{ = }\sqrt[]{8} \end{gathered}`

Using the difference of two squares formulation we can re-write as a multiple of two factors:

`(\text{ x + }(1)/(7))^2\text{ - 8 }\equiv\text{ ( x + }(1)/(7)\text{ + }\sqrt[]{8}\text{ ) }\cdot\text{ ( x + }(1)/(7)\text{ -}\sqrt[]{8}\text{ )}`

Then the factorized equation becomes:

`\text{ ( x + }(1)/(7)\text{ + }\sqrt[]{8}\text{ ) }\cdot\text{ ( x + }(1)/(7)\text{ -}\sqrt[]{8}\text{ ) = 0}`

The solution of the equation becomes:

`\begin{gathered} x\text{ = - }(1)/(7)\text{ - }\sqrt[]{8} \\ \\ x\text{ = }\sqrt[]{8}-(1)/(7) \end{gathered}`

We can condense our solution in the form:

`x\text{ = - }(1)/(7)\pm2\sqrt[]{2}`