Question

Homework: Section 3.4HomeworkQuestion 10, 3.4.43 >HW Score: 90%, 9 of 10 pointsPoints: 0 of 1SaveFind all zeros of the polynomial function. Use the Rational Zero Theorem, Descartes's Rule of Signs, and possibly the graph of the polynomial function shown by agraphing utility as an aid in obtaining the first zero or the first root.f(x)=x²-14x³ +34x² +114x+65Find the zeros of the polynomial function.0(Simplify your answer. Type an exact answer, using radicals and i as needed. Use a comma to separate answers as needed. Type each answer only once.)Help me solve thisView an exampleGet more help.Clear allCheck answer

Answer 1

1) Let's begin with that, by using the Rational Zero Theorem

`\begin{gathered} f(x)=x^4-14x^3+34x^2+114x+65 \\ \\ (dividers\:of\:the\:independent\:term)/(dividers\:of\:leading\:coefficient)=(\pm1,5,13,65)/(\pm1) \\ \\ Plug\:x=-1 \\ \left(-1\right)^4-14\left(-1\right)^3+34\left(-1\right)^2+114\left(-1\right)+65=0 \\ 0=0\:True! \\ Plug\:x=1 \\ 1^4-14\cdot \:1^3+34\cdot \:1^2+114\cdot \:1+65=0 \\ 200=0\:False \\ Plug\:x=-5 \\ \left(-5\right)^4-14\left(-5\right)^3+34\left(-5\right)^2+114\left(-5\right)+65=0 \\ 2720=0\:False \\ Plug\:x=5 \\ 5^4-14\cdot \:5^3+34\cdot \:5^2+114\cdot \:5+65=0 \\ 360=0\:False! \\ Plug\:x=-13 \\ \left(-13\right)^4-14\left(-13\right)^3+34\left(-13\right)^2+114\left(-13\right)+65=0 \\ 63648=0\:False \\ Plug\:x=13 \\ 13^4-14\cdot \:13^3+34\cdot \:13^2+114\cdot \:13+65=0 \\ 5096=0\:False! \\ Plug\:x=-65 \\ \left(-65\right)^4-14\left(-65\right)^3+34\left(-65\right)^2+114\left(-65\right)+65=0 \\ 21831680=0\:False \\ Plug\:x=65 \\ 65^4-14\cdot \:65^3+34\cdot \:65^2+114\cdot \:65+65=0 \\ 14157000=0\:False \\ \end{gathered}`

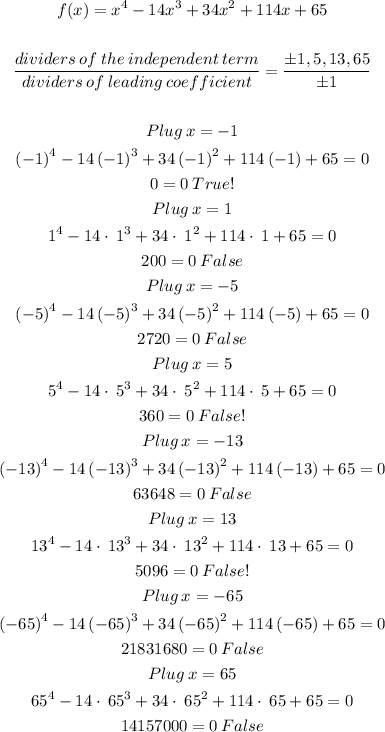
So, with the Rational Zero Theorem method, we could only find one root.

x=-1

2)Now, let's apply the Descartes' Rule of Signs

`\begin{gathered} Enlisting\:the\:coefficients\:we^(\prime)ve\:got: \\ \\ 1,-14,34,114,65 \end{gathered}`

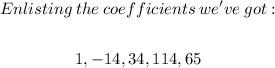
Note that there are two sign changes, so there are two or no

positive roots