Question

The two-way table shows the number of people whose hobbies are reading or solving puzzles and who either ride a motorcycle or don’t ride a motorcycle.

Among people whose hobby is reading, what is the relative frequency of not riding a motorcycle? Express your answer as a decimal, and round to the nearest hundredth if necessary.

Answer 1

Relative frequency is the frequency of a particular outcome, in this case, reading/not riding a motorcyle, divided by the total number of people asked. 7+3+5+9= 24

5/24=.208

Answer 2

The relative frequency of people whose hobby is reading and is not riding a motorcycle is 0.42 (approx)

Explanation:

Relative frequency is the fraction of number of favorable outcome by total possible outcomes that is

`\text{ Relative frequency}=\frac{\text{number of favorable outcome}}{\text{total possible outcomes}}`

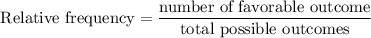
Since, we have to find the relative frequency of people whose hobby is reading and is not riding a motorcycle.

From the given data,

Number of people whose hobby is reading are ( 7 +5) = 12

Number of people whose hobby is reading and is not riding a motorcycle is 5.

`\text{ Relative frequency}=\frac{\text{Number of people whose hobby is reading and is not riding a motorcycle}}{\text{Number of people whose hobby is reading}}`

`\text{ Relative frequency}=(5)/(12)=0.41666..`

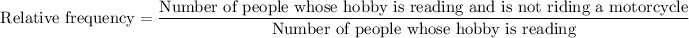
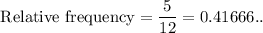
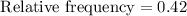`\text{ Relative frequency}=0.42`(approx)

Thus, the required relative frequency of people whose hobby is reading and is not riding a motorcycle is 0.42 (approx)