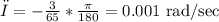Question

Hi thank goodness yea I am and thank everyone thank

Answer 1

The statement pertains to English and involves themes of gratitude, self-realization, and identity, suitable for a college-level discussion. It reflects a personal journey towards living authentically as oneself, which is a common theme in literature and personal narrative studies.

Step-by-step explanation:

The provided statement reflects upon a personal journey and the fulfillment of living as one's true self. In this context, being grateful is an emotional response that acknowledges the positive aspects of one's life experiences. When someone expresses that they are grateful their dream came true, it implies that a deep aspiration or desire was realized, bringing them joy and satisfaction. Within English studies, particularly in the realms of literature or personal development, such expressions often lead to discussions about identity, personal transformation, and the importance of self-acceptance.

The concept of living as 'Michael, the man I was born to be' suggests a journey towards self-realization and authenticity. It can evoke themes common in the study of English, including character development and narrative arcs that pertain to an individual's search for identity. Whether this is through the study of characters in literature or the exploration of personal narratives in writing classes, these themes are central to understanding how individuals come to terms with who they are.

Given that this statement is more reflective and experiential rather than factual information, the subject is classified as English because it pertains to expression and can lead to a discussion about literary themes of identity and the human condition. The statement might come from a college student because of the level of self-reflection and understanding that is typically expected at the collegiate level in humanities courses.

Answer 2

Given a figure represents the distance between an airplane and a radar station on the ground.

We will find the following:

Step 1: we will find a relation between x and θ

As shown we may consider the triangle which a right-angle triangle

With the height = 3000 ft

And the side (x) is the adjacent side to the angle θ

the side (3000) is the opposite side to the angle θ

so, we can write the following equation:

`\begin{gathered} tan\text{ }θ=(opposite)/(adjacent) \\ \\ tan\text{ }θ=(3000)/(x)\rightarrow x=\frac{3000}{tan\text{ }θ} \end{gathered}`

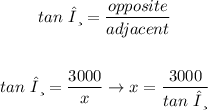
Step (2): at the instant x = 2000 ft, we will compute the following:

`\begin{gathered} x=2000 \\ θ=tan^(-1)((3000)/(x))\approx56.31\degree \end{gathered}`

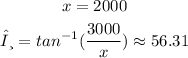
Also, we will find the first derivative of x and θ

`\begin{gathered} x=(3000)/(tanθ)=3000*cot\text{ }θ \\ \\ (dx)/(dt)=3000*(-csc^2θ)*(dθ)/(dt) \end{gathered}`

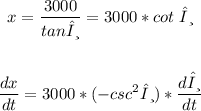
the value of (dx/dt) is given and equal to 200 ft/sec

Substitute dx/dt and θ to find dθ/dt

`\begin{gathered} 200=3000*(-csc^256.31)*(dθ)/(dt) \\ \\ (dθ)/(dt)=-(200)/(3000*csc^256.31)=-(3)/(65) \end{gathered}`

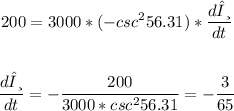
So, the answer to step (2) will be as follows:

`\begin{gathered} x=2000\text{ }ft \\ (dx)/(dt)=200\text{ ft/sec} \\ θ=56.31\degree \\ (dθ)/(dt)=-(3)/(65)\text{ deg/sec} \end{gathered}`

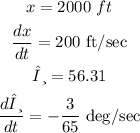
Step (3):

We will find how fast the radar is rotating

Which will be the angular velocity ω

`ω=(d\theta)/(dt)=-(3)/(65)\text{ deg/sec}`

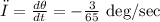
convert from degree to radian

`ω=-(3)/(65)*(\pi)/(180)=0.001\text{ rad/sec}`