Answer:
There are 7 quarters and 9 nickels.
Step-by-step explanation:
Let the number of quarters = x
Let the number of nickels = y
There are a total of 16 coins, therefore:
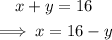
• 1 Quarter = $0.25
,
• 1 Nickel =$0.05
Since the total value in the cup is $2.20, we have that:
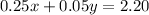
We substitute x in the first equation into the second one.
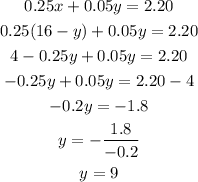
Recall: x=16-y
Therefore:
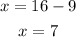
There are 7 quarters and 9 nickels.