Question

Quarters and nickels, a total of sixteen. How many of each, without being seen?The value of two-twenty is right in this cup. You will find the answer, a certain cheer up. Make a table, a graph, an equation will do. Give it a try and learn something new. It's a challenge I know, but don't give up hope. The answer is obtainable and within your scope.quarters is x and nickels is y

Answer 1

There are 7 quarters and 9 nickels.

Step-by-step explanation:

Let the number of quarters = x

Let the number of nickels = y

There are a total of 16 coins, therefore:

`\begin{gathered} x+y=16 \\ \implies x=16-y \end{gathered}`

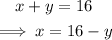
• 1 Quarter = $0.25

,

• 1 Nickel =$0.05

Since the total value in the cup is $2.20, we have that:

`0.25x+0.05y=2.20`

We substitute x in the first equation into the second one.

`\begin{gathered} 0.25x+0.05y=2.20 \\ 0.25(16-y)+0.05y=2.20 \\ 4-0.25y+0.05y=2.20 \\ -0.25y+0.05y=2.20-4 \\ -0.2y=-1.8 \\ y=-(1.8)/(-0.2) \\ y=9 \end{gathered}`

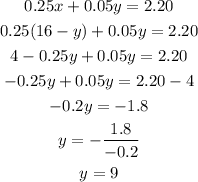
Recall: x=16-y

Therefore:

`\begin{gathered} x=16-9 \\ x=7 \end{gathered}`

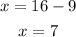
There are 7 quarters and 9 nickels.