Question

10Suppose that the time required to complete a 1040R tax form is normal distributed with a mean of 90 minutes and a standard deviation of 10 minutes. What proportion of 1040R tax forms will be completed in more than 71 minutes? Round your answer to at least four decimal places.

Answer 1

To determine the proportion is the same as determining the probability that the tax form will take more than 71 minutes to be completed, that is, we are looking for the probability:

`P(X>71)`

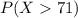
To determine this probability we need to notice that this normal distribution has mean 90 and standard deviation 10; once we know this we can use the z-value to use the standard normal ditribution. The z-value is:

`z=(x-\mu)/(\sigma)`

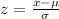
Then in this case we have:

`z=(71-90)/(10)=-1.9`

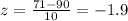
Then we have that:

`P(X>71)=P(Z>-1.9)`

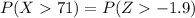
Finally, using a standard distribution table we have that:

`P(Z>-1.9)=0.9713`

Therefore, 0.9713 (which is 97.13%) of the forms will take more than 71 minutes to complete.