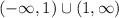Question

Show all work such as a table on finding the domain and range of L(x)= (x-1)/(x+3)

Answer 1

`\begin{gathered} Domain:(-\infty,-3)\cup(-3,\infty) \\ Range:(-\infty,1)\cup(1,\infty) \end{gathered}`

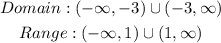
Explanation:

Given the function:

`l(x)=(x-1)/(x+3)`

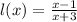
Domain

The domain of a function is the set of the values of x at which the function is defined.

A rational function is undefined when its denominator equals 0.

`\begin{gathered} x+3=0 \\ x=-3 \end{gathered}`

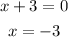
Therefore, the domain of l(x) is:

`(-\infty,-3)\cup(-3,\infty)`

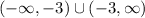
Range

The range of a function is the set of the values of L(x) at which the function is defined.

Since L(x) is a rational function, find the horizontal asymptote.

`Horizontal\;Asymptote,y=1`

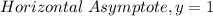
Therefore, the range of the function is:

`(-\infty,1)\cup(1,\infty)`