Question

A 2.90-kg block is released from rest and allowed to slide down a frictionless surface and into a spring. The far end of the spring is attached to a wall, as shown. The initial height of the block is 0.500 m above the lowest part of the slide and the spring constant is 443 N/m. A. What is the maximum compression of the spring?B. The spring sends the block back to the left. How high does the block rise?

Answer 1

Part (a)

The potential energy of the block due to its height can be given as,

`U=\text{mgh}`

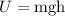
The potential energy due to presence of spring can be expressed as,

`U=(1)/(2)kx^2`

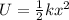
Equating both the values,

`\begin{gathered} \text{mgh}=(1)/(2)kx^2 \\ x^2=(2mgh)/(k) \\ x=\sqrt[]{(2mgh)/(k)} \end{gathered}`

Substitute the known values,

`\begin{gathered} x=\sqrt[]{\frac{2(2.90kg)(9.8m/s^2)(0.500\text{ m)}}{(443\text{ N/m)}}(\frac{1\text{ N}}{1kgm/s^2})} \\ \approx0.253\text{ m} \end{gathered}`

Thus, the maximum compression of the spring is 0.253 m.

Part (b)

Since the slide is frictionless, therefore no energy loss happened during the sliding of block. Therefore, the block will rise up to the same initial height which is 0.500 m.