Question

The mean percentage of a population of people eating out at least once a week is 57% with a standard deviation of 3.50%. Assume that a sample size of 40 people was surveyed from the population a significant number of times. In which interval will 68% of the sample means occur?

between 55.89% and 58.11%
between 56.45% and 57.55%
between 56.54% and 57.46%
between 56.07% and 57.93%

Answer 1

The correct answer is "between 56.45% and 57.55%." The mean percentage of a population of people eating out at least once a week is 57% with a standard deviation of 3.50%. Assume that a sample size of 40 people was surveyed from the population a significant number of times. At interval between 56.45% and 57.55%, 68% of the sample means to occur.

Answer 2

Answer: between 56.45% and 57.55%

Step-by-step explanation:

We are given:

μ = population mean = 57%

σ = population standard deviation = 3.50%

n = sample size = 40

CL = confidence level = 68% = 0.68

We need to calculate the confidence interval in which we should find the sample mean
`\bar{x}`.

First of all, we need to calculate the sample standard deviation:

`s = (\sigma)/(√(n) ) = (3.50)/(√(40) )`

s = 0.55

Now, there are two equivalent ways to arrive to the answer:

1) short way: use the Empirical Rule, also known as 68–95–99.7 Rule, to remember that 68% of the data lies within 1 standard deviation from the mean.

Therefore, the confidence interval should be:

`\mu - 1 s \leq \bar{x} \leq \mu + 1 s`

57 - 0.55 ≤
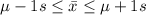
`\bar{x}` ≤ 57 + 0.55

56.45 ≤
`\bar{x}` ≤ 57.55

2) long way: make all the calculations.

First, find the critical value corresponding to the confidence level required:

`1 - (\alpha )/(2) = 1 - (1 - CL)/(2) = 1 - (1 - 0.68)/(2) = 0.84`

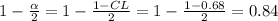
Now, since the sample size is greater than 30 and it is said to be statistical significant, we can use a z-score table (instead of a t-score table).

Looking for which z-score corresponds to a probability closest to 0.84, we get z = 1.00 (which confirms the Empirical Rule).

Now, we can find the confidence interval requested:

`\mu - z \cdot s \leq \bar{x} \leq \mu + z \cdot s`

57 - 1·0.55 ≤
`\bar{x}` ≤ 57 + 1·0.55

56.45 ≤
`\bar{x}` ≤ 57.55