Question

Multiple-Object Accelerating Systems: As shown in the figure, two blocks are connected by a very light string, and the upper block is pulled upward by a different string. The masses of the upper and lower blocks are m1 = 300 g and m2 = 240 g, respectively. The tension in the upper string is equal to 6.6 N.a) Find the acceleration of the system.b) Find the tension in the lower rope.

Answer 1

Part A.

To get the acceleration of the system we consider the two blocks as a single mass. For this situation we have, from Newton's second law, that:

`T-W=(m_1+m_2)a`

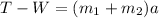
where T is the tension in the upper sting and W is the weight of the system. Solving the equation for a we have:

`\begin{gathered} 6.6-(0.3+0.24)(9.8)=(0.3+0.24)a \\ a=(6.6-(0.3+0.24)(9.8))/((0.3+0.24)) \\ a=2.42 \end{gathered}`

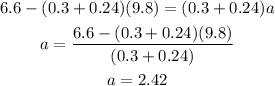
Therefore the acceleration of the system is 2.42 meters per second per second.

Part B.

Now, that we have the acceleration of the system we analyze the lower block individually; for this block the equation of motion is:

`T^(\prime)-W^(\prime)=m_2a`

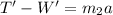
where T' is the tension in the lower rope, W' is the weight of the lower block and m2 is its mass. Solving for the tension we have that:

`\begin{gathered} T^(\prime)=(0.24)(9.8)+(0.24)(2.42) \\ T^(\prime)=2.93 \end{gathered}`

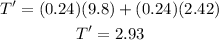
Therefore the tension in the lower rope is 2.93 N