Question

Two equations are shown: • Equation 1: 3 4 (x−12)=12 •Equation 2: 3 4 y−12=12 Solve each equation. Then, enter a number in each box to make this statement true. The value of x is: The value of y is:

Answer 1

`x=28`

`y=32`

Explanation

Let's solve each equation step by step

Equation 1:
`(3)/(4) (x-12)=12`

Step 1. Distribute
`(3)/(4)`

`(3)/(4) x-(3)/(4) *12=12`

`(3)/(4) x-9=12`

Step 2. Add 9 to both sides

`(3)/(4) x-9+9=12+9`

`(3)/(4) x=21`

Step 3. Multiply both sides of the equation by
`(4)/(3)`

`(3)/(4) x*(4)/(3)=21*(4)/(3)`

`x=28`

Equation 2:
`(3)/(4) y-12=12`

Step 1. Add 12 to both sides

`(3)/(4) y-12+12=12+12`

`(3)/(4) y=24`

Step 2. Multiply both sides by
`(4)/(3)`

`(3)/(4) y*(4)/(3)= 24*(4)/(3)`

`y=32`

Answer 2

The required value of x = 28

The required value of y = 32

Explanation:

The given two equations are :

`(3)/(4)(x-12)=12..........(1)\\\\(3)/(4)\cdot y-12=12...........(2)`

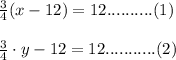
Now, we need to solve both the equations and find out the required values of both the unknowns x and y.

Solving equation (1) to obtain value of x. We have,

`(3)/(4)(x-12)=12\\\\\text{On cross multiplication, we get}\\\\\implies 3* (x-12)=12* 4\\\implies 3x -36=48\\\implies 3x=48+36\\\implies 3x=84\\\bf\implies x=28`

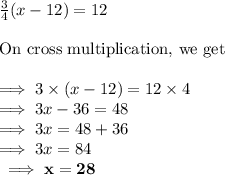
Solving equation (2) to obtain value of y. We have,

`(3)/(4)\cdot y-12=12\\\\\implies (3)/(4)\cdot y=12+12\\\\\implies (3)/(4)\cdot y=24\\\\\text{On cross multiplicatrion, We get}\\\implies 3\cdot y=24* 4\\\implies 3y = 96\\\bf\implies y=32`

Hence, The required value of x = 28

And The value of y = 32