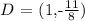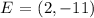Question

Graph the function below. Plot 5 points on the graph of the function, one point with x equals zero, two points with negative x values, and two points with positive x values.

Answer 1

Let the function:

`y\text{ = }(-11)/(8)x^3`

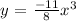
Since it is a cubic function, its graph is

now, the points on the graph, that are requested are obtained as follows:

For x= 0 then

`y=f(0)=(-11)/(8)(0^3)=0`

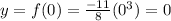
thus, the point with x equals zero is:

`A\text{ = (0,0)}`

now, for x = -1 then:

`y=f(-1)=(-11)/(8)(-1^3)=(11)/(8)`

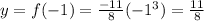
thus, a point with a negative x value is:

`B\text{ =(-1,}(11)/(8)\text{)}`

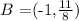
also, for x = -2, we get:

`y=f(-2)=(-11)/(8)(-2^3)=11`

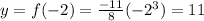
then, another point with a negative x value is:

`C\text{ = (}-2,11\text{)}`

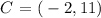
now, if x = 1, then

`y=f(1)=(-11)/(8)(1^3)=(-11)/(8)`

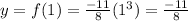
thus, a point with a positive x value is:

`D\text{ = (1,-}(11)/(8)\text{)}`

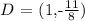
also, if x = 2, we get:

`y=f(2)=(-11)/(8)(2^3)=-11`

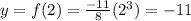
then, another point with a positive x value is:

`E\text{ = }(2,-11)`

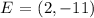
On the graph, these points are:

So that, we can conclude that the correct answer is:

The graph of the function is:

one point with x equals zero is:

`A\text{ = (0,0)}`

two points with negative x values are:

`B\text{ =(-1,}(11)/(8)\text{)}`

`C\text{ = (}-2,11\text{)}`

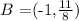
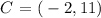
two points with positive x values are:

`D\text{ = (1,-}(11)/(8)\text{)}`

`E\text{ = }(2,-11)`