Question

The hypotenuse of a 45-90 right triangle is 10 square root 2. The legs are what?

Answer 1

Statement Problem: Find the other legs of a 45-45-90 right triangle whose hypotenuse side is;

`10\sqrt[]{2}`

Solution:

Since the base angles are equal to 45 degrees, then the legs are equal. So, the opposite side is equal to the adjacent side.

Let the adjacent side and opposite side be x;

Now, we would apply the pythagoras theorem stated as;

`\begin{gathered} h^2=o^2+a^2 \\ \text{Where h = hypotenuse, o = opposite and a = adjacent;} \end{gathered}`

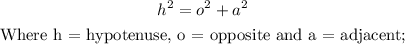
Thus, we have;

`\begin{gathered} (10\sqrt[]{2})^2=x^2+x^2 \\ 100(2)=2x^2 \\ 2x^2=200 \\ x^2=(200)/(2) \\ x^2=100 \\ x=\sqrt[]{100} \\ x=10 \end{gathered}`

CORRECT OPTION: C, none of these