We are given the following information.
Radius of first beach ball = r₁ = 8 inches
Radius of second beach ball = r₂ = 16 inches
To find out how much material do we need to make each of these beach balls, we need to find out their the surface area.
Recall that the surface area of a sphere is given by
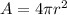
Where r is the radius of the sphere.
The surface area of the first beach ball is
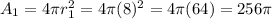
The surface area of the second beach ball is

So the surface area of the first beach ball is 256π in²
The surface area of the second beach ball is 1024π in²
The ratio of their surface area is
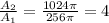
Therefore, we can conclude that the surface area of the second beach ball is 4 times the surface area of the first beach ball.
Twice the amount of material used to make the first beach ball is not enough to make the second beach ball.
You will need 4 times the amount of material used for the first beach ball to make the second beach ball.
A₂ = 4A₁