Question

Using a table of values, what is the approximate positive solution to the equation /(I) = g(I| to the nearest quarter of a

Answer 1

Step-by-step explanation:

Given:

`\begin{gathered} f(x)\text{ = log\lparen x + 2\rparen} \\ g(x)\text{ = 4}^x\text{ - 1} \end{gathered}`

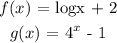
To find:

To use the table of values to get the approximate positive solution to the equation

For f(x) = g(x)

`log(x\text{ + 2\rparen= 4}^x\text{ - 1}`

using table of values, we will assume values for x:

let x = 0.05, 0.25, 0.75

`\begin{gathered} when\text{ x = 0.05} \\ log(0.05+2)\text{ = 4}^(0.05)\text{ - 1} \\ 0.3118\text{ = 0.072} \\ \\ when\text{ x = 0.25} \\ log(0.25+2)\text{ = 4}^(0.25)\text{ - 1} \\ 0.352\text{ = 0.414} \\ \\ when\text{ x= 0.75} \\ log(0.75+2)\text{ = 4}^(0.75)\text{ - 1} \\ 0.439\text{ = 1.828} \end{gathered}`

For the approximate value to be a solution, the result on the left-hand side will be close to or equal to the result on the right-hand side.

From the values used, only x = 0.25 has a close value

To ascertain that the result is correct, graphing the equation gives 0.214 as the right value of x

But the question asked that the result is to the nearest quarter of a unit (this include values such as 0.25, 0.5, and 0.75).

As a result, the approximate positive solution to the equation to the nearest quarter of a unit is x ≈ 0.25 (option A)