Question

-8Intro-4-2864yf(x) = 3 (2)48XConsider the exponential function: f(x) = 3[*The initial value for this function is VThe base for this function is

Answer 1

Step-by-step explanation:

The function is given below as

`f(x)=3((5)/(4))^x`

Concept:

An exponential function is a function in which the variable is an exponent. Exponential functions are written in the form f(x)=ab^x f ( x ) = a. b^ x . Initial Value: The initial value of an exponential function is the result of substituting x=0 into the function.

Hence,

by putting x=0, we will have the initial value be

`\begin{gathered} f(x)=3((5)/(4))^(x) \\ f(0)=3((5)/(4))^0 \\ f(0)=3 \end{gathered}`

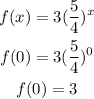
Hence,

The initial value is

`3`

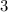
Part B:

The genral equation of an exponential equation is given below as

`\begin{gathered} y=ab^x \\ a=constant \\ b=base \end{gathered}`

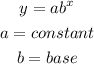
By comparing coefficnets,

The base for this function is

`(5)/(4)`

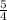
Part C:

The domain of the function is given below as