We have a function with an exponetial form:
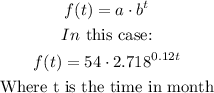
The initial value is when t=0 (means 0 month), so:
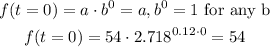
When the researcher started the number of birds was 54. This discard the second and the last option.
And, we can find the concept of b taking the ratio of f(t) for two different values of t:
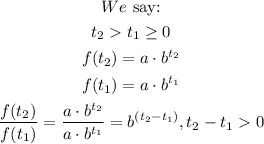
So, the base b is related with the growth of the population, if b is greater than 1 the population increase with time, if b is less than 1 the population decrease with time.
So, the correct answer is the first option.