Question

The four sequential sides of a quadrilateral have lengths a = 3.1, b = 6.5, c = 7.1, and d = 8.5 (allmeasured in yards). The angle between the two smallest sides is a = 95.What is the area of this figure?area =yd?Your answer should be accurate to 4 decimal places.

Answer 1

The diagram of the given figure is:

To find the area we can start by dividing the quadrilateral into two triangles:

Now, we can find the areas of Triangle 1 and Triangle 2.

We can use the law of cosines to find the third side of the Triangle 1.

Given a=3.1, b=6.5 and the angle C=95, use the formula:

`h^2=a^2+b^2-2ab\cdot\cos C`

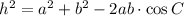
By replacing the values we obtain:

`\begin{gathered} h^2=3.1^2+6.5^2-2(3.1)(6.5)\cdot\cos 95 \\ h^2=9.61+42.25-40.3\cdot(-0.0872) \\ h^2=55.3724 \\ h=\sqrt[]{55.3724} \\ h=7.4413 \end{gathered}`

And the Area of triangle 1 can be calculated using the Heron's formula as:

`\begin{gathered} A1=\sqrt[]{s(s-a)(s-b)(s-h)} \\ s=(a+b+h)/(2)=(3.1+6.5+7.4413)/(2)=8.52065 \\ A1=\sqrt[]{8.52065(8.52065-3.1)(8.52065-6.5)(8.52065-7.4413)} \\ A1=10.0368 \end{gathered}`

Now, to calculate the Area of Triangle 2, knowing the 3 sides, we can use the same formula:

`\begin{gathered} s=(c+d+h)/(2)=(7.1+8.5+7.4413)/(2)=11.5207 \\ A2=\sqrt[]{11.5207(11.5207-7.1)(11.5207-8.5)(11.5207-7.4413)} \\ A2=25.0511 \end{gathered}`

Then, the total area is the sum of the area1 and area2:

`\begin{gathered} At=A1+A2=10.0368+25.0511 \\ At=35.0879 \end{gathered}`

Answer: The area of this figure is 35.0879 yd^2