As per given by the question,
There are given that the two point, (0, 0) and (5, 12).
Now,
We need to find the distance of this point from the center, using Pythagoras theorem.
That means,
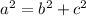
Then,
From the given point,
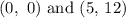
The given point 5 and 12 are the x and y values respectively of the point.
Then,
The x and y axex are right angle to each other.
So,
From the formula,
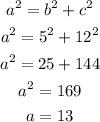
So, the radius of the circle is 13.
Hence, the option A is correct.