Question

The annual rainfall in a certain region is approximately normally distributed with mean 41.2 inchesand standard deviation 6.1 inches. Round answers to the nearest tenth of a percent.a) What percentage of years will have an annual rainfall of less than 43 inches? %b) What percentage of years will have an annual rainfall of more than 38 inches? %c) What percentage of years will have an annual rainfall of between 37 inches and 42 inches?%

Answer 1

To solve the question, first, we have to standardize the data, meaning, we will compute the z-scores that correspond to 43, 38, 37, and 42.

Z-scores:

`\begin{gathered} Z_(43)=(43-41.2)/(6.1)\approx0.29508, \\ Z_(38)\approx-0.52459, \\ Z_(37)\approx=-0.68852, \\ Z_(42)\approx0.13115. \end{gathered}`

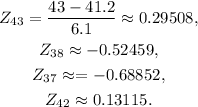
Now, using tables, we get the area under the normal curve that corresponds to each z-score to get the percentages for questions a, and b:

a) x<43 corresponds to 0.61603, therefore, 61.60% is below 43 inches.

b) x>38 corresponds to 0.70007, therefore, 70.01% is above 38 inches.

Now, using tables, we get that:

x<37 corresponds to 0.24556, and x<42 corresponds to 0.55217, therefore

`0.55217-0.24556`

corresponds to the interval between 37 and 42 inches.

Answer:

a) 61.60%,

b) 70.01%,

c) 30.67%.