To solve the question, first, we have to standardize the data, meaning, we will compute the z-scores that correspond to 43, 38, 37, and 42.
Z-scores:
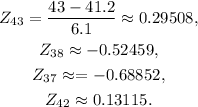
Now, using tables, we get the area under the normal curve that corresponds to each z-score to get the percentages for questions a, and b:
a) x<43 corresponds to 0.61603, therefore, 61.60% is below 43 inches.
b) x>38 corresponds to 0.70007, therefore, 70.01% is above 38 inches.
Now, using tables, we get that:
x<37 corresponds to 0.24556, and x<42 corresponds to 0.55217, therefore

corresponds to the interval between 37 and 42 inches.
Answer:
a) 61.60%,
b) 70.01%,
c) 30.67%.