Question

The sphere at the right fits snugly inside a cube with 4-in. edges. What is the approximate volume of the space between the sphere and cube?

Answer 1

As given by the question

There are given that the inside edge is 4 in.

Now,

Since sphere fits snugly inside a cube therefore diameter of sphere will be equal to side of the cube

So,

`\begin{gathered} \text{diameter}=4\text{ inches} \\ \text{radius}=(dameter)/(2) \\ \text{radius}=(4)/(2) \\ \text{radius}=2 \end{gathered}`

Then,

Volume of the sphere is given by:

`\begin{gathered} (4)/(3)*\pi* r^3=(4)/(3)*3.14*2^3 \\ =(4)/(3)*3.14*8 \\ =33.5 \end{gathered}`

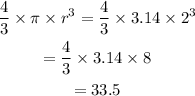
And,

The volume of a cube is:

`\begin{gathered} \text{Volume of cube=side}* side* side \\ =4*4*4 \\ =64\text{ inches} \end{gathered}`

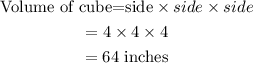
Then,

The volume of the space between the sphere and cube = 64-33.5 = 30.5.

Hence, the answer is 30.5 cube inches.