Question

Fernando has locked himself out of his house. He needs to borrow a ladder from a neighbor to reach an unlocked window on the second floor that is 8 (ft.) above the ground. To avoid some landscaping under the window, he must set the base of the ladder 6 (ft.) away from the foundation of the house.What does the length of the ladder need to be to reach the window?

Answer 1

We can draw the situation as follows:

We have here a right triangle with two known legs. We can apply the Pythagorean Theorem to find the hypothenuse of the triangle, and, thus, the length of the ladder need to reach the window.

We know that:

`c^2=a^2+b^2\Rightarrow c^2=6^2+8^2\Rightarrow c^2=36+64\Rightarrow c^2=100`

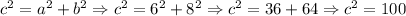
If we take the square root to both sides of the equation, we finally have:

`\sqrt[]{c^2}=\sqrt[]{100}\Rightarrow c=10`

Then, the length of the ladder needs to be 10 ft to reach the window.