Answer:
The liquid in this barometer would be 8416.393 milimeters.
Step-by-step explanation:
Since hydrostatic pressure is directly proportional to fluid density (
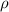 ), measured in grams per mililiter, and height of fluid (
), measured in grams per mililiter, and height of fluid (
 ), measured in milimeters. Two barometers with distinct fluids are equivalent when both have the same hydrostatic pressure. Then, we construct the following relationship:
), measured in milimeters. Two barometers with distinct fluids are equivalent when both have the same hydrostatic pressure. Then, we construct the following relationship:
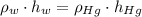 (1)
(1)
Where:
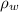 ,
,
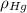 - Densities of fluid and mercury, measured in grams per mililiter.
- Densities of fluid and mercury, measured in grams per mililiter.
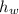 ,
,
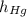 - Heights of fluid and mercury columns, measured in milimeters.
- Heights of fluid and mercury columns, measured in milimeters.
If we know that
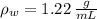 ,
,
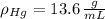 and
and
 , then the liquid level of this barometer is:
, then the liquid level of this barometer is:
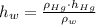
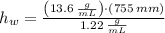
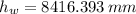
The liquid in this barometer would be 8416.393 milimeters.