We must find the value k such that Q(x) = (x+2) is a factor of the cubic polynomial:
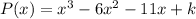
Now, if (x+2) is a factor of the polynomial P(x), then the rest R of the following division must be zero,
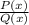
So we must compute the division between the polynomials and check the condition to have R = 0. We compute the quotient by applying the method of synthetic division. Doing that we have:
From the division we see that the rest is:
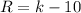
The condition is that the rest R must be equal to zero, so:
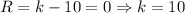
Answer: k = 10