Question

What's the vertex for 6x^2-48x-54=0?

Answer 1

y = 6x²-48x-54 has a vertex at (4,-150)

Explanation:

There is no vertex. The solution set to 6x²-48x-54 = 0 is two points, (-1,0) and (9,0).

If you mean y = 6x²-48x-54, that is an up-opening parabola.

Put the equation into vertex form:

y = 6x²-48x-54

 = 6(x²-8x)-54

 = 6(x²-8x+4²)-6·4²-54

 = 6(x-4)² - 150

vertex at (4,-150)

Answer 2

Hello!

`\large\boxed{(4, -150)}`

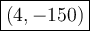
We can solve for the vertex by completing the square. Begin by factoring out 6 from the equation to simplify the process:

6(x² - 8x) - 54 = 0

To complete the square, we must look at the first two terms (x² - 8x).

Remember that squaring a binomial uses the format a² + 2ab + b². We are already given a² and 2ab², so solve for b:

-8 / 2 = -4. This is the value of b.

We can rewrite this as:

(x - 4)²

However, this produces +16 which much be taken into account. Substitute (x - 4)² into the original equation:

6(x - 4)² - 54 = 0

Multiply 16 by the term in the front and subtract to cancel out this term:

6(x - 4)² - 54 - (6 · 16) = 0

Simplify:

6(x - 4)² - 150 = 0

In this form, the vertex is given as:

a(x - h)² + k, where h = x-coordinate and k = y-coordinate of the vertex.

In this instance, h = 4 and k = -150, so the coordinates of the vertex are:

(4, -150)