Question

A uniform ladder whose length is 5.2 m and whose weight is 400 N leans against a frictionless vertical wall. The coefficient of static friction between the level ground and the foot of the ladder is 0.35. What is the greatest distance the foot of the ladder can be placed from the base of the wall without the ladder immediately slipping

Answer 1

the greatest distance the foot of the ladder can be placed from the base of the wall without the ladder immediately slipping is 3.3424 m

Explanation:

Given the data in the question and as illustrated in the images below;

without the ladder immediately slipping, the net torque and the net force mus all balance out.

from the first image;

In the x, the force is;

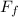`F_(f)` = N₂

mg = N₁

the torque about the ground contact point gives the following equation

N₂Lsin∅ = mgcos∅
`(L)/(2)`

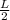
solving for ∅

tan∅ = mg / 2N₂ 55

∅ = tan⁻¹ ( mg / 2N₂ )

we already know that N₂ =
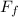`F_(f)` = μN₁ = μmg

so,

∅ = tan⁻¹ ( mg / 2μmg )

∅ = tan⁻¹ ( 1 / 2μ )

given that; The coefficient of static friction between the level ground and the foot of the ladder μ = 0.35

we substitute

∅ = tan⁻¹ ( 1 / (2×0.35 ) )

∅ = tan⁻¹ ( 1.42857 )

∅ = 55°

now to get the required distance;

from the second image; cos∅ = d / L

d = Lcos∅

given that; length of the ladder = 5.2 m

we substitute

d = 5.2cos(50)

d = 3.3424 m

Therefore, the greatest distance the foot of the ladder can be placed from the base of the wall without the ladder immediately slipping is 3.3424 m