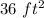Question

Miles has a square garden in his backyard. He decides to decrease the size of the garden by 1 foot on each side in order to make a gravel border. After he completes his gravel border, the area of the new garden is 25 feet2. In the equation (x - 1)2 = 25, x represents the side measure of the original garden. Whats the length and area?

Answer 1

6 and 36

Explanation:

Answer 2

Let

x-------> the length side of the original square garden

Step 1

Find the value of x

we know that

`(x-1)^(2)=25`

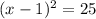
taking square root both sides

`(x-1)=(+/-)√(25)`

`(x-1)=(+/-)5`

`x1=1+5=6\ ft`

`x2=1-5=-4\ ft`

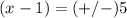
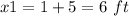
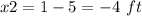
the solution is

`x=6\ ft`

therefore

the answer Part a) is

The original length side of the square garden is
`6\ ft`

Step 2

Find the area of the original square garden

we know that

the area of the original square garden is equal to

`A=x^(2)`

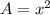
substitute the value of x in the formula

`A=6^(2)=36\ ft^(2)`

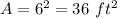
therefore

the answer part b) is

the area of the original square garden is
`36\ ft^(2)`