Question

Given the points A(0, 0), B(e, f), C(0, e) and D(f, 0), determine if line segments AB and CD are parallel, perpendicular or neither.

parallel
perpendicular
neither

Answer 1

Given the points, when point A, B, C, D are plotted, and connect AB and CD to form a segment, they are not neither parallel nor perpendicular. 

Answer 2

we have that

`A(0, 0)\\B(e, f)\\ C(0, e)\\D(f, 0)`

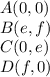
we know that

If two lines are parallel

then

their slopes are equals

and

if two lines are perpendicular

then

the product of their slopes is equal to
`-1`

step 1

find the slope of the line segment AB

`m=((y2-y1))/((x2-x1))`

`mAB=((f-0))/((e-0))`

`mAB=((f))/((e))`

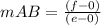
step 2

find the slope of the line segment CD

`m=((y2-y1))/((x2-x1))`

`mCD=((0-e))/((f-0))`

`mCD=((-e))/((f))`

`mAB*mCD=((f)/(e) )*((-e)/(f) )\\ =-1`

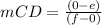
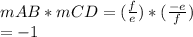
therefore

the answer is

Line segments AB and CD are perpendicular